相信大家都知道我们经常在深度学习评价指标中常用的精度、召回率、准确率以及ROC曲线,我之前对部分指标的理解还是不到位,所以这里再次把更直观的解释展示出来,方便大家理解
关于TP 、 FP、 TN以及FN
假设当前一张图像样本里总共包括230个行人,现在对图像中的行人进行检测,结果检测出来100个目标框,其中60个框检测到了行人,其余40个框没有检测到行人

根据上图
$$
TP = 60,FP=40, FN=230-60=170
$$
所以
精度Precision
$$
precision=\frac{TP}{TP+FP}=\frac{60}{60+40}=0.6
$$
召回率Recall
$$
recall=\frac{TP}{TP+FN}=\frac{60}{60+170}≈0.26
$$
举一个图像实例
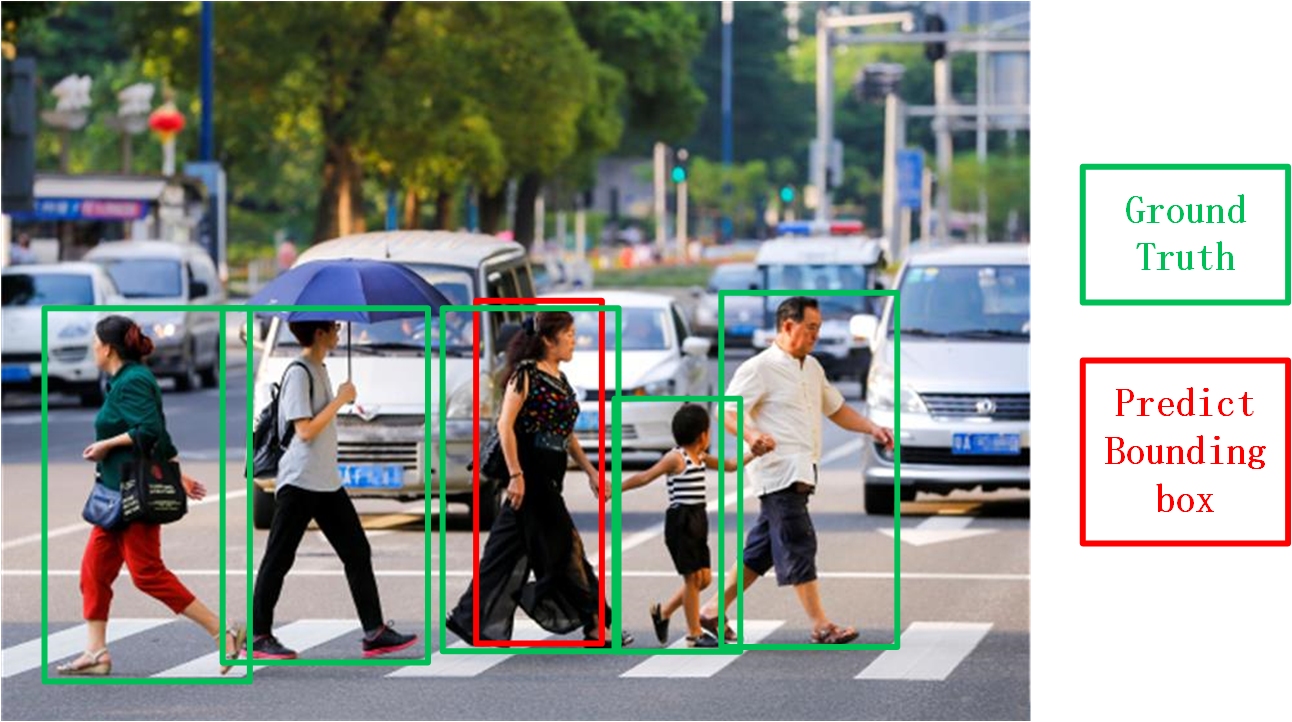
$$
precision=\frac{TP}{TP+FP}=\frac{1}{1+0}=1
$$
$$
recall=\frac{TP}{TP+FN}=\frac{1}{1+4}=0.2
$$
为什么说仅仅精度无法有力说明网络模型的检测能力呢?
假设上面的例子里样本总共包含2300个目标,对样本中的目标进行检测,结果检测出来100个目标框,其中60个框检测到了目标,其余40个框没有检测到目标。
那么,
$$
precision=\frac{TP}{TP+FP}=\frac{60}{60+40}=0.6
$$
$$
recall=\frac{TP}{TP+FN}=\frac{60}{60+1700}≈0.026
$$
可以看出,精度在两种情况下没有变化,而召回率则差异巨大,所以要综合指标进行考量。
目标检测下IoU与FP、TP的关系


延伸扩展
平均精度AP(average precision)
AP: AP at IoU= 0.50: 0.05: 0.95
含义:一般情况下通常使用的IoU取值0.5,0.05指step, 0.95指自己确定阈值范围的最大阈值。那么AP即指从0.5到0.95,每0.05步长取一个阈值对数据集中的每张图片进行单个类别目标检测,得到一组所有样本的precision值,当把这10组精度值都得到之后,再取其平均值,即可得到AP.
$$
AP^{50},即指当IoU取值0.5时的数据集中的每张图片的单个类别目标检测的精度先求和再求其平均值。
$$
$$
AP^{75},即指当IoU取值0.75时的数据集中的每张图片的单个类别目标检测的精度先求和再求其平均值。
$$
mAP(mean average precision)
含义:当IoU取某个定值时的数据集中的每张图片的所有类别目标检测的精度先求出每种类别的AP再求和最后求其平均值。
通常赛事中的评价指标以及含义可参见下图
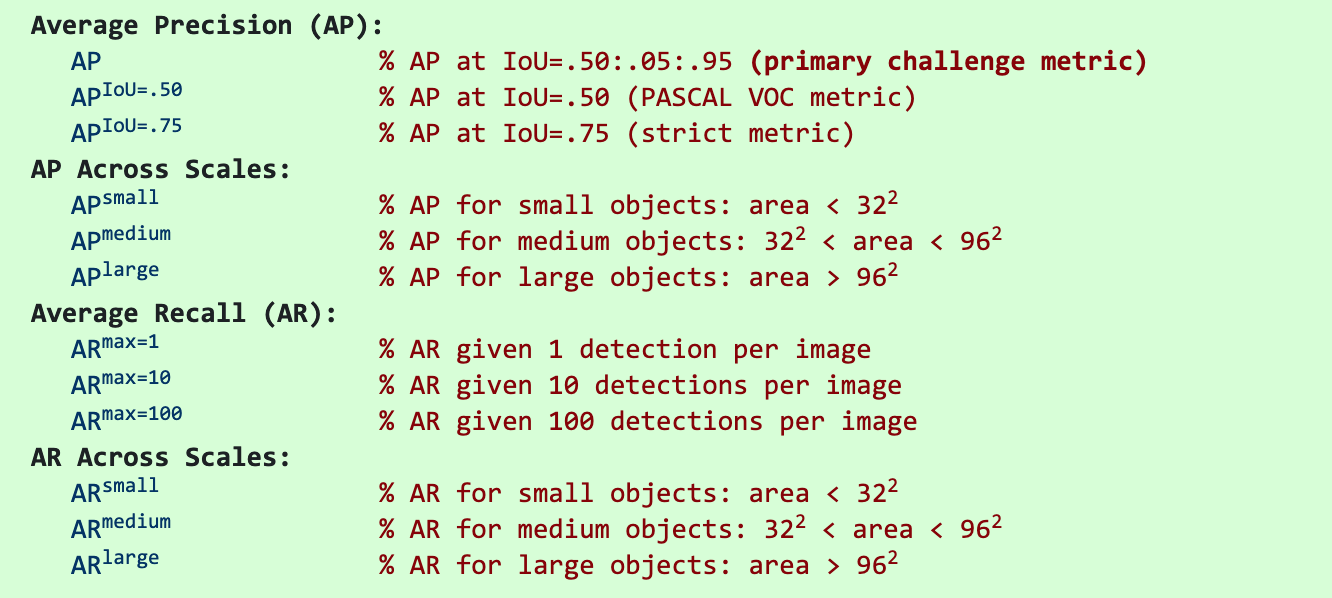
准确率
$$
accuracy=\frac{TP+TN}{TP+TN+FP+FN}=\frac{TP+TN}{Total}
$$
F-Score
分别比较两个模型的精度和召回率比较困难得出哪个模型更好,因此,为了使它们具有可比性,建议使用F-Score
$$
F_{score} = \frac{2\ast precision\ast recall}{precision + recall}
$$
ROC(Receiver operating characteristic)曲线
显示分类模型在所有分类阈值下的效果的图表。
X轴:真正例率 True Positive Rate,简称TPR
$$
TPR=\frac{TP}{TP+FN}
$$
Y轴:假正例率 False Positive Rate,简称FPR
$$
FPR=\frac{FP}{FP+TN}
$$
这里我给出一组例子方便大家更具体的理解ROC曲线:假定现在有总数为100的样本,其中正样本50张,负样本50张,现在要对样本进行分类,首先在阈值设定为0.3的时候,得到每张图像的分类结果,进行统计,再设定阈值为0.5对所有样本进行分类并统计,最后设定阈值为0.7对所有样本进行分类并统计,这样我们便会得到三组当在不同阈值下的分类统计数表。具体表格内容如下图: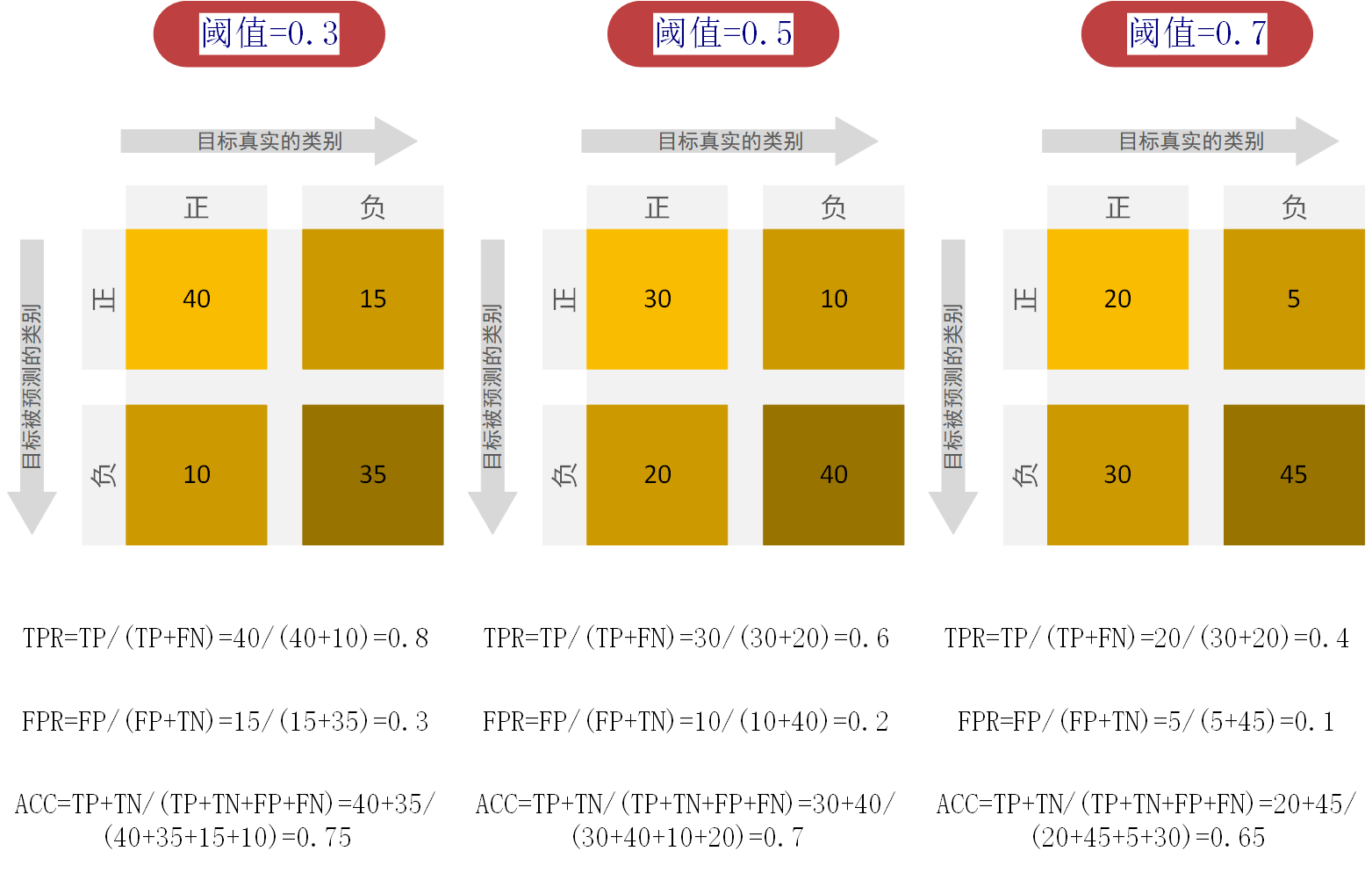
当然,你也许会问,这些数据背后的逻辑是什么呢?或者有什么隐含的关系吗?
我们不妨推理一下,当阈值设的越低的时候,是不是有更多的样本会被分类为正样本,即更多的正样本被分类为正样本,更多的负样本被分类为正样本,那么TP与FP的数值应该是随着阈值的降低而增大的,那么相应的,因为正样本与负样本的各类的总数是没有变化的,所以正样本被认为是负样本的数量即FN是减少的,负样本被认为是负样本的数量即TN也是减少的。
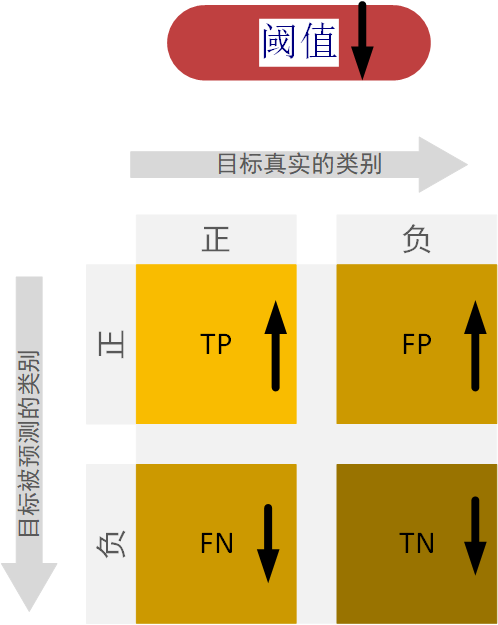
反映在曲线图上即如下图所示:
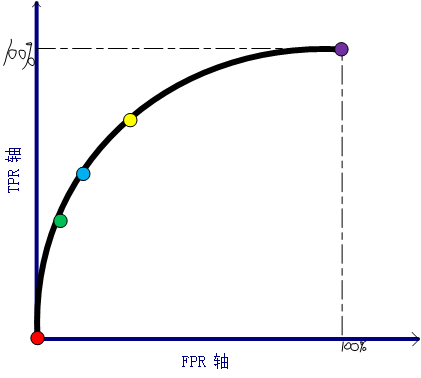
我以上图红点、绿点、蓝点、黄点以及紫点进行说明:黄点代表阈值为0.3的分类结果,蓝点代表阈值为0.5的分类结果,绿点代表阈值为0.7的分类结果。
(1)将同一模型每个阈值 的 (FPR, TPR) 座标都画在ROC空间里,就成为特定模型的ROC曲线。
(2)红点:当阈值设置的足够大时,分类为正样本的数量理论上接近于0,即包括TP=0以及FP=0,那么对应的TPR=0,FPR=0,对应到上图,相当于坐标轴的(0,0)点,则可得出红点对应的是阈值足够大的分类情况。
反之,当当阈值设置的足够小时,分类为正样本的数量理论上达到最大,相当于TP=所有的正样本数,FP=所有的负样本数,那么此时的TPR=1,FPR=1,对应到上图,相当于坐标轴的(1,1)点,则可得出紫点对应的是阈值足够小的分类情况。
(3)越靠近左上角准确度越高
当FPR=0时,得出FP=0,那么TPR=TP/(TP+0)=1, 又因为所有正样本都被分为正,那么正样本被分为负的数量就是0,即FN=0, 对应到图中,正确;那么此时的准确度ACC=(TP+TN)/(TP+FP+TN+FN)=(TP+TN)/(TP+0+TN+0)=1,所以证明了越靠近左上角的点准确度越高。同理可证,离右下角越近的点,预测越不准。
(4) 随着阈值降低,ROC上的点向右上方移动,随着阈值变大,ROC上的点向左下方移动。