关于卷积的运算过程相信大家已经读过各种各样的解释了,本文旨在以图示的方法从浅到深由单张图像到多张图像的卷积的图示形象的向大家解释卷积的基本原理,从单通道到多通道在卷积过程中输入到输出的具体映射都可以看到,相信在阅读本文之后,大家对卷积会有更直观的认识
关于卷积
基本术语
卷积核——kernel 、 filter
填充——padding
滑动步长——slides
通道数——channel
特征映射——feature map
张量——tensor
卷积过程
相信大家对于二维数据的卷积形式已经很熟悉了,也知道了卷积的具体本质相当于矩阵乘法。这里我们直接以图像的表述方式来向大家展现卷积在神经网络中的过程。
这里首先是对几个张量的说明:
当我们输入1张长度为4宽度为4通道为4的图像时,我们可以表述输入为
[要处理的图像数量,每张图像的高度,每张图像的宽度,每张图像的通道数] 即[batch, in_height, in_width, in_channels]
或许有人会疑惑?为什么图像的通道可以为4或者更大,我们以往知道的都是3通道啊?
是的,通常我们常见的是3通道的图像,至于4通道的图像是可以人为定义第四通道的数据的,比如令第四通道=0或者第四通道=第一二三的任意组合,都是可以的,以此类推,更多通道的也是可以参照理解。我记得曾经有一篇论文就是网络的输入是4通道的数据,其中第四通道=resize(第一通道)+resize(第二通道)+resize(第三通道)+0,可能文字不太好理解,具体可参见下图:
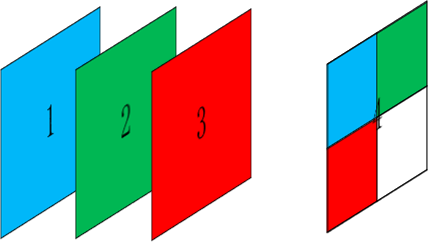
那么单张图像的张量形式可以表示为:
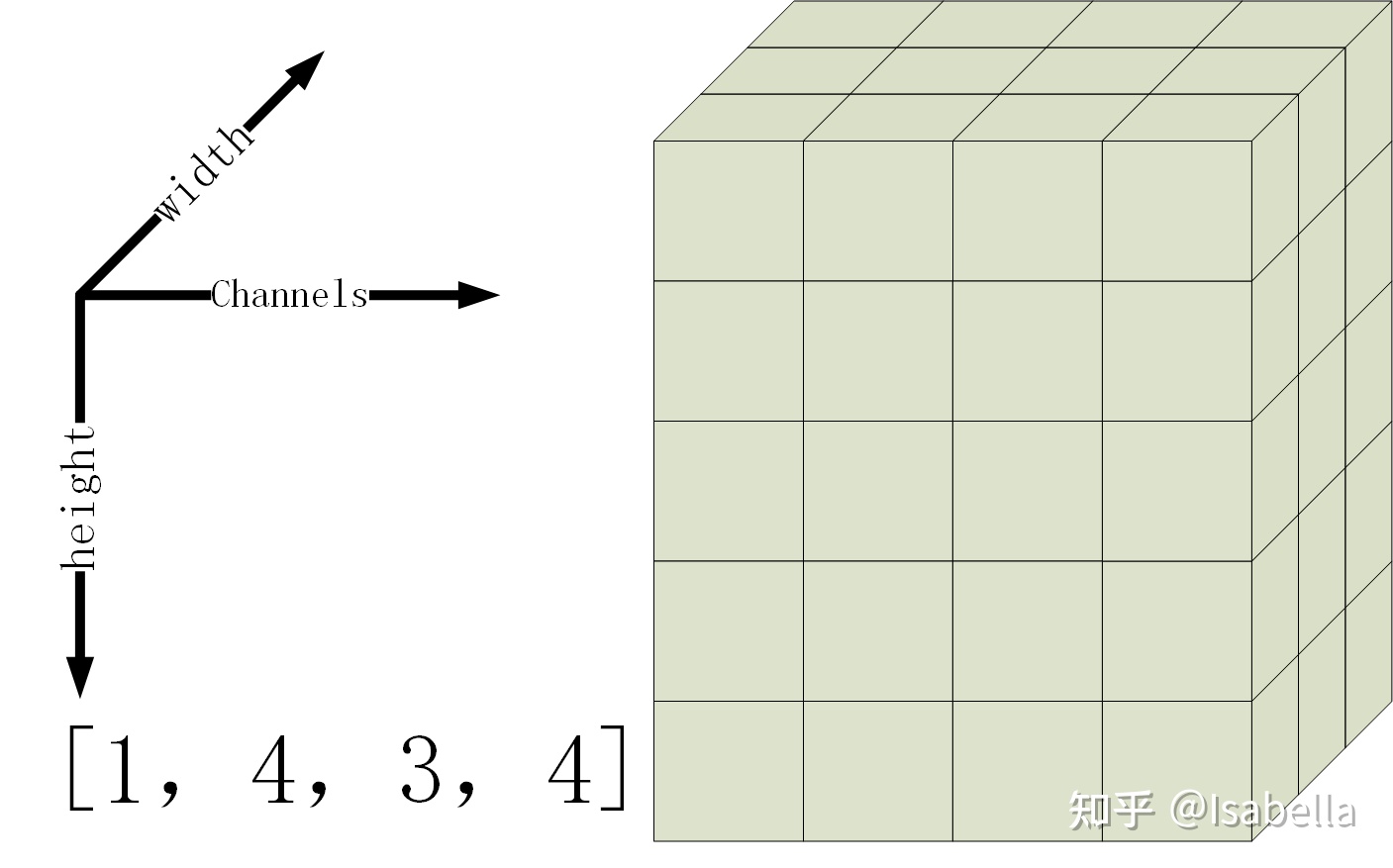
其次是卷积核(也称滤波器)的张量形式为
[卷积核高度,卷积核宽度,输入图像的通道数,卷积输出的通道数],即[filter_height, filter_width, in_channels, out_channels]
out_channels即是卷积之后的feature_map的通道数,也是卷积核的个数
那么多个卷积核的张量形式可以表示为:
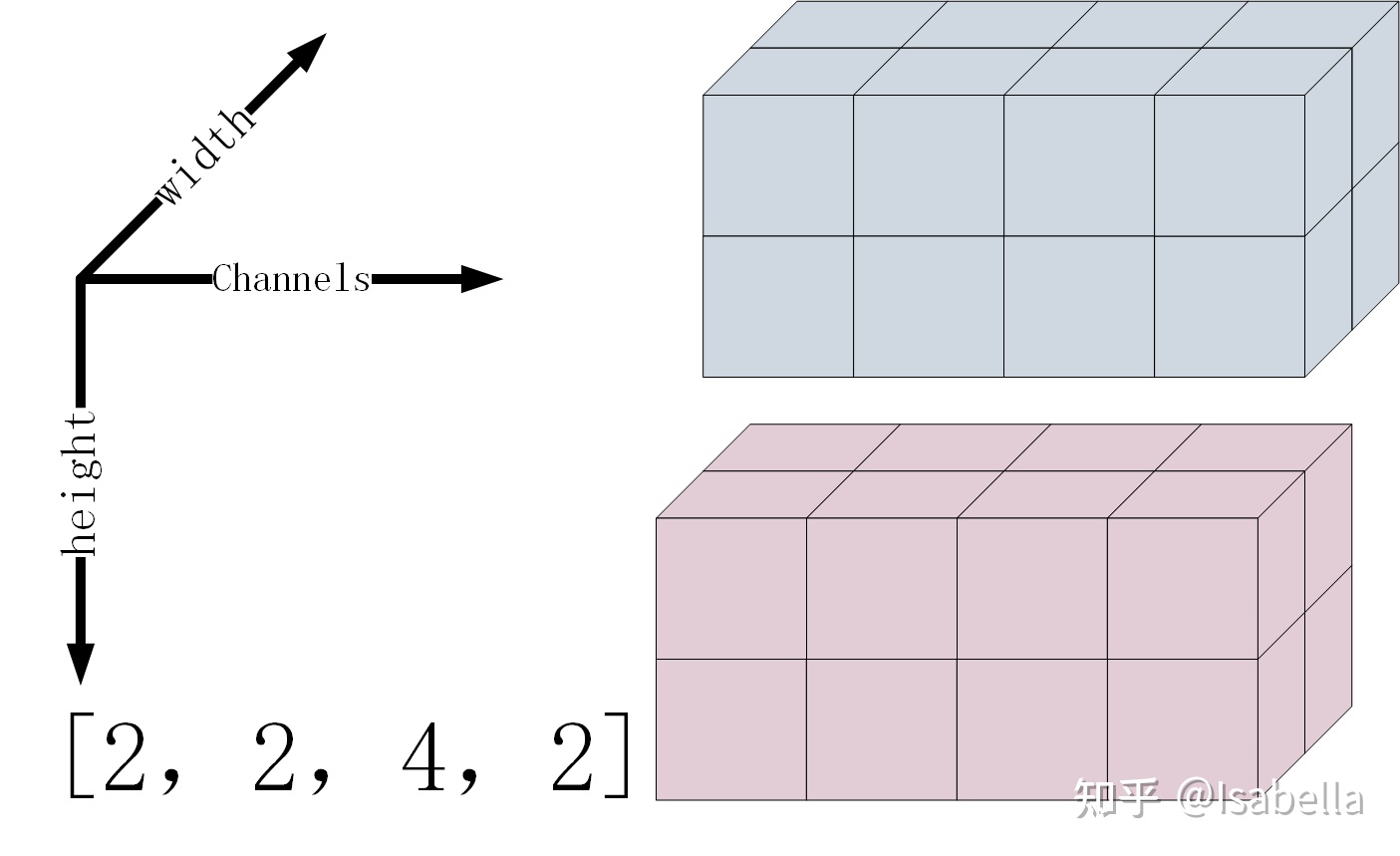
具体卷积过程可以参考下图
首先介绍单张图像输入的卷积过程
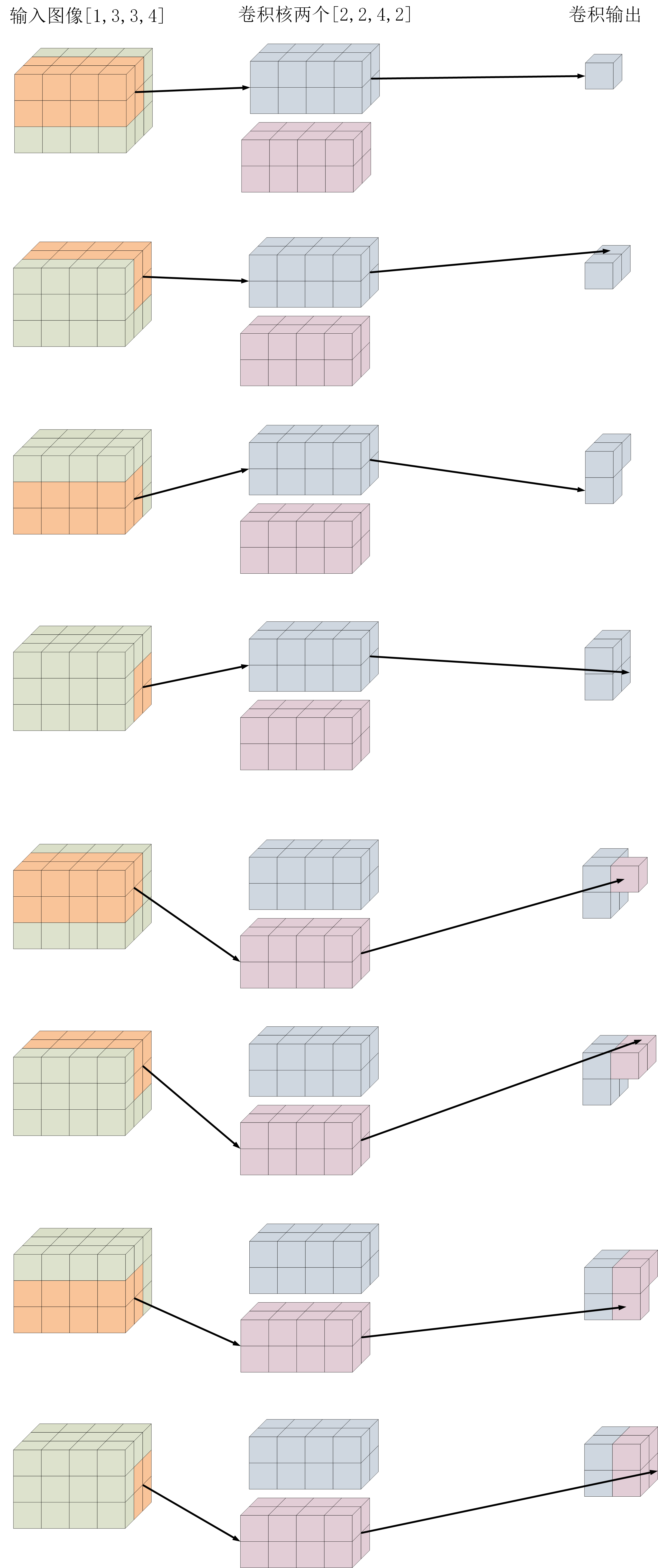
其次介绍多张图像输入的卷积过程

关于卷积的运算
在tensorflow中经常用到的是conv2d函数,我用的版本是1.14,其conv2d的具体形式参见
1 | tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None) |
strides: 长度为4的一维向量,表示在input每个维度上的步长
padding:分为’VALID’与’SAME’
VALID——不对输入图像填充,直接卷积
SAME——表示卷积后的feature_map要与input的size相同(注意size是指[width,height]而不是四维tensor的shape)所以要先对输入图像填充,再卷积
顺便给出卷积后的size计算大小公式,前提输入w_i=h_i, 卷积核 w_f=h_f,每边填充长度为p,步长为s,则卷积后的宽w_o或者高h_o
$$
w_{o}=\frac{w_{i}-w_{f}+2p}{s}+1
$$
关于卷积核尺寸的选择
为什么不建议使用偶数size的kernel?
答:推导过程如下:
$$
\frac{w-f+2p}{s}=w
$$
这里f=2k
$$
\frac{w-2k+2p}{s}=w-1
$$
$$
w-2k-2p=(w-1)s
$$
$$
2p=(w-1)(s-1) +(2k-1)
$$
若s为奇数2m+1,则上式化为:
$$
2p=(w-1)\times2m+(2k-1)
$$
$$
2p=偶数+奇数=奇数
$$
显然不成立!
所以一般不使用偶数size的kernel,从而避免padding不居中的问题
为什么经常使用3×3或5×5的卷积核,而不是7×7或者11×11?
答:推导过程如下:
假设一张单通道的7×7图像进行7×7卷积输出一个值

三种卷积思路都是实现同一种卷积结果,但是可以看出第三种的参数个数最少,相较第一种参数量下降44.8%,这在实际内存中是非常客观的缩减量。
从卷积层的深入在特征映射上的反映:
由此可以看出小尺寸的卷积核不仅降低了参数量,还能随着卷积层的增多,还能抽取更丰富的特征信息