最近回过头来在看《Deep Learning》 这本书,经过三年的工作时间,再看这本书的时候曾经理解不了的问题或者推导原理有了自己切身的认识与思考,所以现在想把自己曾经算是一个半路出家的机器视觉从业者从新手到上手的一些原理性和实践性的点加上我自己的思考把底层的基础点分享出来,帮助大家可以更直观的理解和学习
线性模型最著名的局限性
无法学习异或(XOR)函数,即f([0; 1]; w) = 1 和f([1; 0]; w) = 1,但f([1; 1]; w) = 0 和f([0; 0]; w) = 0。
常用的逻辑函数都有哪些?
与(AND): 输入全1输出1,输入有0输出0
或(OR):输入全0输出0,输入有1输出1
与非(NAND):输入全1输出0,输入有0输出1
或非(NOR):输入全0输出1,输入有1输出0
异或(XOR):输入相同输出0,输入相异输出1
同或(XNOR):输入相同输出1,输入相异输出0
这里我们根据下图更好理解一点:
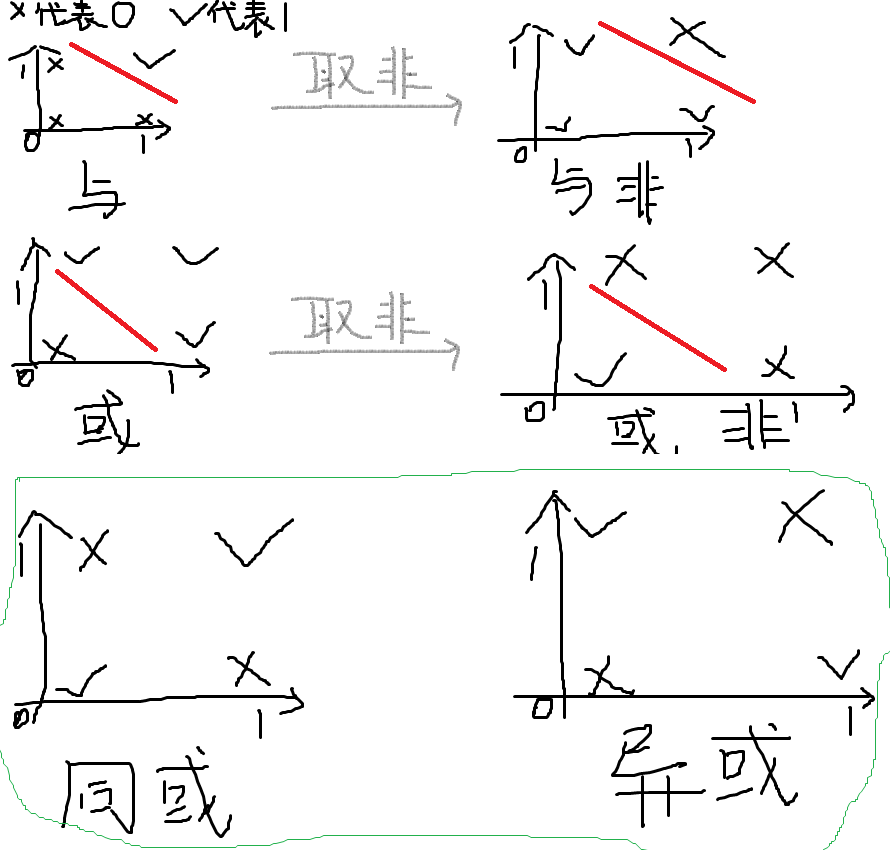
可以看出,与、与非、或以及或非都可以用线性模型来进行分类,也可以根据差异性进行区分,这就类似一种学习能力能够实现分类,所以延伸到深度学习,因为当时的线性模型无法学习同或以及异或函数,这个缺陷在当时难以被接受,便由此引发了神经网络热潮的第一次大衰退。
那么神经网络又是如何解决异或函数的表达问题呢?
首先我们先给出一个最简单的网络模型以及输入输出的表达。
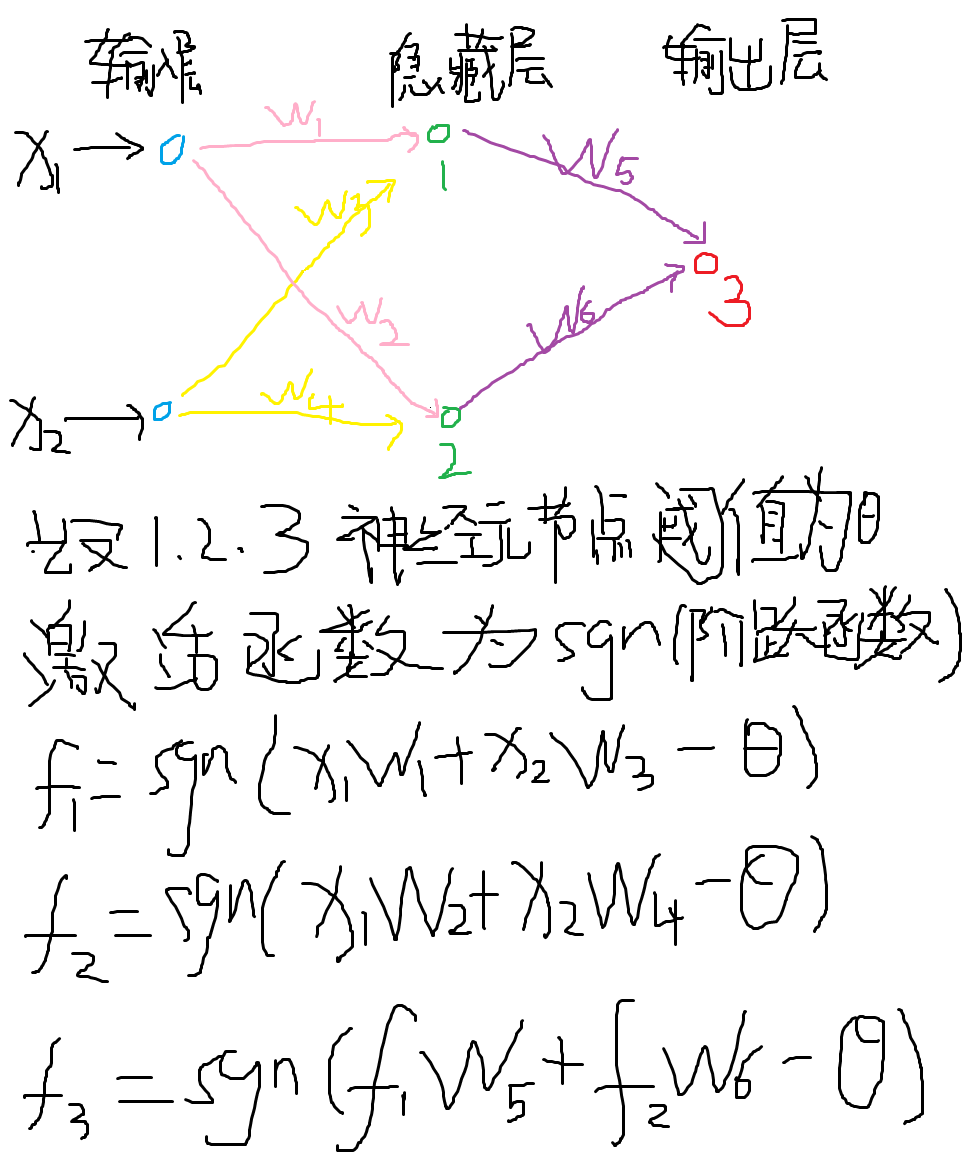
然后,我们根据异或函数的输入输出反推各神经节点的参数值,具体情况如下图推导过程。



至此,我们可以看出,合理的参数取值可以实现异或函数XOR的表达,这个进步完全弥补了线性模型的缺陷,深度学习也因此迎来新一波的学习浪潮。